HOW DOES IT WORK ?

The circle, the line and the point, in combination with the numbers of additions, multiplications or divisions invite us to fabulous discoveries. 

EXAMPLE : THE MULTIPLICATION BY 3 IN NUMBER 7 

For example, we study the multiplication by 3 by means of the progression of the triples: 1, 3, 9, 27, etc., and we draw it on the circumference of  a circle defining N = 7 equidistant points numbered from 1 to N. Then we simply join the defined points by drawing lines according to the order of the value of the terms of the series.
Of course the progression of triples wich is theoretically infinite, is here limited by the number of elements of N. Therefore, when the value of a term of the series is higher than the value of N, we subtract the value of N from the value of the term as many times as necessary. In the same manner we count the hours,  the 26th hour being equivalent to 2 hours. In arithmetic, the terms are said to be congruent to the number N.  The progression 1, 3, 9, 27, etc., is thus transformed into a periodic sequence with 6 terms: 1, 3, 2, 6, 4, 5, 1, etc. (9=9-7=2).  

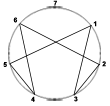
ex 1: the multiplication by 3 in a circle with 7 points 

To represent the multiplication by 3, we join every number to its triple on a circle divided into N points.
Within the circle we draw a line from the point 1 to the point 3, then another one from 3 to 2, another from 2 to 6, etc.:
1 * 3 = 3; a line joins 1 to 3 
2 * 3 = 6; a line joins 2 to 6 
3 * 3 = 9; a line joins 3 to 2 (because 9 - 7 = 2 in a circle with 7 points)

Did you understand ? 
  ex. 2: multipl. by 3 in a circle with 211 points 

Using a larger number of elements on the circle, we'll obtain a better graphic definition (ex.2, multiplication by 3 in a circle with 211 points). We observe that all the straight lines are tangent to a 8-shaped curve named nephroïde.