Chryzode
Un voyage en images dans la science des nombres (arithmétique)
A pictorial travel into arithmetic
Origines des Chryzodes
Déjà, dans des ouvrages de Platon, on retrouve l'utilisation du cercle pour représenter les nombres. Et les bâtisseurs des cathédrales ont sans doute eu recours à un procédé analogue: le cercle, pour représenter les nombres
polygônes étoilés inscriptibles dans une circonférence
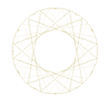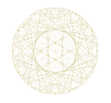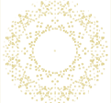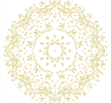
partagée avec 2, 3 et 4 points equidistants
jusqu'à 7 points
jusqu'à 12 points
Prenons un exemple :
Sur le cercle, pour représenter le nombre 2, nous déterminons
un point origine puis nous plaçons un deuxième point que nous relions
par un trait au point origine.
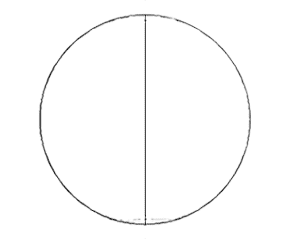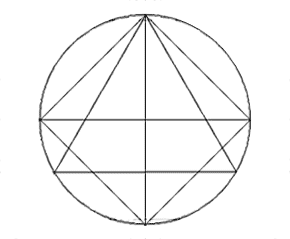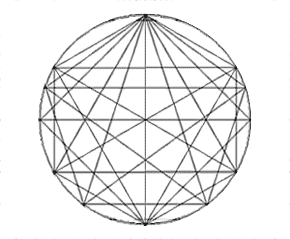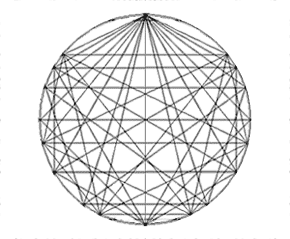
Pour représenter le nombre 3, on place 3 points équidistants.
On relie ces 3 points et on obtient un triangle.
Il est utile de garder
la même origine, tout comme le zéro sert bien de point de
départ pour étudier l'échelle des nombres.
Pour le nombre 4, on place 4 points qui, lorsqu'ils sont reliés,
dessinent un carré plus une croix.
< L'image obtenue est représenté ci-contre. Notons que ce dessin figure dans certaines peintures du moyen-âge, par exemple des gravures de Dürer.
Pourquoi ne pas poursuivre ce procédé au delà de 4 points ?
Curieux comme tout chercheur, nous avons perseveré et tenté la superposition avec tous les polygônes étoilés inscriptibles dans une circonférence partagée avec 5 points, puis 6 points, 7 points, 8 points, etc.
< Dans la figure ci-contre on a représenté tous les nombres jusqu'au nombre 7.
Dans la figure ci-dessous on a représenté tous les nombres jusqu'au nombre 12, c'est à dire la superposition de tous les polygônes étoilés inscriptibles dans des cercles partagés de 2 à 12 points.
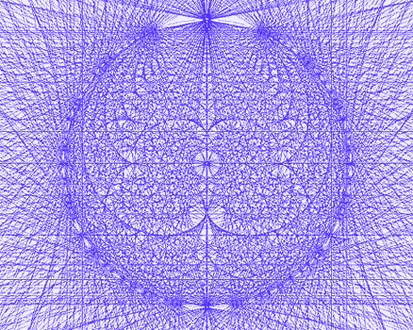jusqu'à 17 points [Cliquez sur l'image]