Maintaining, on a same figure we superimpose modules having an increasing
number of elements, that is to say integers series 2, 3, 4, etc.
Thus, on the circle, to represent number 2, we determine a
point origin, then we place a second point which we connect by a line.
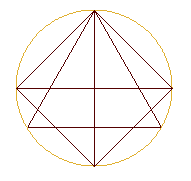
To represent number 3, 3 equidistant points are placed. One connects
these 3 points and one obtains a triangle. Of course, it is useful to keep
the same origin, just as the zero is used as starting point to study the
scale of numbers. For number 4, one places 4 points which, when they are
connected, draw a square more a cross, etc.
The figure thus obtained is represented opposite. |
ex.2
|
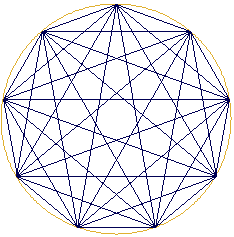
Why not continue this process beyond 4 points? Curious as a researcher
can be, we persevered and superimposed the set of the star polygons on
our graph in a circumference divided into 4 points, 5 points, then 6, 7
points, like in the example 3 opposite.
ex 3
|
 |
Opposite, we then represented the integers until number 14. In other
words, we carried out the superposition of all the star polygons in a circle
divided into from 2 to 14 points.
Very quickly we here discover a new type of representation.
ex.4
|
 |
In a more drastic way, we note that superimposing the networks highlights
a series of hypocycloidic envelopes (within the circle). Extending the
lines out of the circle, we should also have observed the presence of epicycloidic
curves (external to the circle).
It should be noted that this type of structure does not seem to
be fractal a priori (in the strict sense) for, if one extends the
graph, one always discovers the fitting of straight and caustic lines,
but does not get the departing structure.
ex.5
|
 |
The instrument makes possible to carry out and discover innumerable
new figures. Also, the team of search with which I work on the subject,
proposes that one calls these graphes chryzodes (1987). This word "CHRYZODE"
is deduced from "chryzos" ( writing out of gold) and "zoi" (circle). It
would mean a golden writing on a circle. For us, it designates the
large family of shapes resulting from the representation of numbers by
means of vectors (and of intersections of these vectors) inscribed on a
graduated circumference.
D-4- First stage:
SCAFFOLDING
Let us come back to the previous example to see that the extreme tangle
of the network suggestes an underlying logical ordering. For that purpose,
applying the arithmetical series to the system makes emerge as a kind of
basic alphabet . Its handling enables to discover a very rich world hardly
explored. It gives us informations too about the structures, the
resonances, the harmonies and the harmonics of the undulatory systems.
First let us here make out two fundamental stages at least : the
construction and the points of intersection.
For the construction we place "m" equidistant points on the cicumference
of a circle (m represents a number). We then connect these points by lines
according to an arithmetical operation.
Multiplication by 2 in number 19
Example
Multiplication by 2 in number 19 : that is to say the geometric
representation in a circle divided into m equal parts of a series
of numbers defined by a multiplicative progression (in geometric progression).
We call that number m "module-circle m" or "circular referential
in value m". We simply say it represents the module m. The example
below illustrates m= 19.
To draw this series of doubles, we use a circumference on which
we first have defined m equidistant points numbered from 1 to m.
Two representations can be used :
- either on the circle we connect each element to its double,
- or we connect the points of the circumference by lines segments
according to the order of the terms of the series.
The progression of doubles theorically infinite will of course here
be limited by the number m. Thus, each time the value of a term
of the series is higher than the value of m, the value of m is substracted
as many times as necessary from this term. (One does not differently
count the hours when the 26 th hour is equivalent to 2 hours: on a clock
in 24 elements we have counted 26 - 24 = 2 hours.). In mathematics
that is said the terms of the series are congruent to the module m.
In this way the progression of doubles 1, 2, 4, 8, 16, 32, 64, 128,
etc., congruent to number 19, becomes a periodical series of 18 terms:
1, 2, 4, 8, 16, 13, 7, 14, 9, 18, 17, 15, 11, 3, 6, 12, 17, 10, 1, 2, 4,
...
On the circle we draw a line which goes from the point 1 to the
point 2, another one from the point 2 to the point 4, and thus, until all
the terms of the series are connected. Let's note the vectors are all tangent
to a remarkable curve, the cardioide, and the network is hamiltonian, the
point numbered 19 being also zero.
2*10=1 modulo 19 |
ex.6 |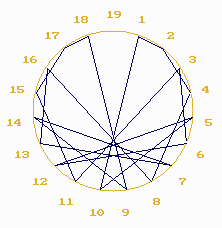
Analysing the process let us note that from the 18th term the series
has become periodical and that we are back at the departing point.
Going over this circuit in the opposite direction (1, 10, 5, 12,
etc.) we notice that it corresponds to the series of multiples of 10 congruent
to the module 19. In other words, we observe that, congruent to the module
19, the series of multiplications by 2 turns into the series of multiplications
by 10.
In arithmetic, that is said 2 is the inverse of 10 in the module 19.
That is 2 * 10 = 1 modulo 19, this is here an expression of the
Fermats' theorem
( when n is prime, n(m-1)=1 et nm-2=1/n ).
In a musical extrapolation, one would say that by number 19, the harmonies
of 2 turn into harmonies of 10. Viewed from this angle, the chryzodes would
seem to be like a representation, an image of this verse-inverse transformation
or harmonization.
| Multiplication by 3 in number 19
Another example :
Let 's study the series of triples, that is : 1, 3, 9, 27, 81, etc.
Congruent to number 19, this progression of triples turns into a
periodical sequence of 18 terms: 1, 3, 9, 8, 5, 15, 7, 2, 6, 18, 16, 10,
11, 14, 4, 12, 17, 13, 1, 3, etc.
Here, the inverses of the powers 3 are the powers 13
that is : 3 * 13 = 1 modulo 19.
On the circle we draw a line which goes from the point 1 to the point
3, then another one from the point 3 to the point 9, and so on until all
the terms of the series are connected. |
ex.7 |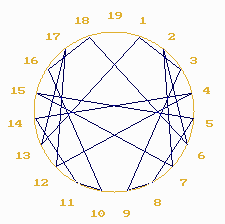
| Multiplication by 3 in number 211
Using a graduated circle with a larger number of elements, a better
graphic definition of the present structure is obtained.
Opposite, is represented the series of triples in number 211.
3 * 142 = 1 MOD 211
|
ex.8 |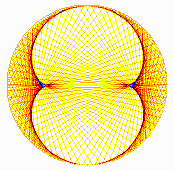
Let us notice that with the multiplication by 3, the straight lines
are all tangent to another cycloidal curve. This one, eight shaped, is
called "nephroide".
Actually, every multiplicative progression in the chryzode generates
a number of points of inflection with one unity less than the value of
the progression. However, the case is different when the value of the series
approaches the value of the number.
Thus, in the series of the multiples of 209 congruent to number
211, the shape will be epicycloidic, it will be a three external retrogressions
astroide.
D-5- Second stage: POINTS OF INTERSECTION.
When long series of numbers are represented, the graph in lines becomes
overloaded and it is no longer very exploitable. On the other hand, if
one wants to illustrate the discontinuous, the corpuscular aspect of the
system, it is shrewd to make only the points of intersection of the vectors
of the chryzode in lines appear and that, by the means of computer.
Multiplication by 3 in the number 2701
The example 9 opposite shows the points of intersection of the vectors
resulting from the series of triples in number 2701. As regards the diffusion
of the points on the graph, here one easily notices necks, moireings, etc
shaped curves .
We soon make many discoveries and the chryzode in points of intersection
takes an inedite relief both by its aesthetic aspect and by the
properties it allows to show. |
ex9 |
D-6- Harmonic superposition of networks
Going on our investigations, we notice that the details of the shapes
resulting from the multiplication by 3 depend on the value of the numbers
in which the multiplication is represented.
Multiplication by 3 in the numbers multiple of 7
For example, opposite is the superposition of the chryzodes resulting
from the multiplications by 3 in some numbers multiple of 7 ( m
= 7, 14, 21, 28, 35, etc.).
We thus observe the emergence of sorts of synchronization beams.
The number of
beams is proportional to the pitch of the sequence (here 7).
We could say that here
we go over the harmonies of 3 at the rate 7.
It is quite plausible to consider that the appearing beams relate
to the harmonics of the vibratory system. (harmonics = multiple
frequencies of a fundamental frequency 7, 14, 21, etc.) |
ex.10 |
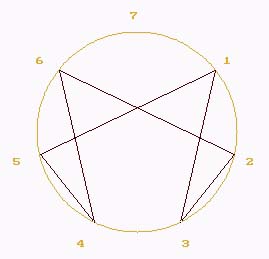
| Multiplication by 3 in number 7
Let us note the coincidences between the main beams of the
chryzode in points in the example 10, and the lines of the chryzode in
lines of the multiplication by 3 in number 7(opposite),that is the series
1, 3, 2, 6, 4, 5, 1. This synchronization is understable because
the chryzode of the multiplication by 3 in number 7 is present in every
superimposed elementary chryzode.
Viewed from this angle, the chryzodes in lines are comparable to
a network, a generic graph, of the chryzode representing the harmonics
networks.
3 * 5 =1 MOD. 7
ex 11
|
 |
| Enlarging the multiplication by 3 in numbers multiple
of 7
Enlarging a part from the example 10 we observe a sort of overlapping
system linking the different beams between each other.
Example. 12 : a part of the ex. 10 enlargement |
ex.12 |
D-7-1-Synchronization beams at a
molecular level
As part of a cognitive approach, the dicovery and the modelization
of the synchronization beams by superposition of networks are worth our
attention. Actually, we have here like a bridge to better understand the
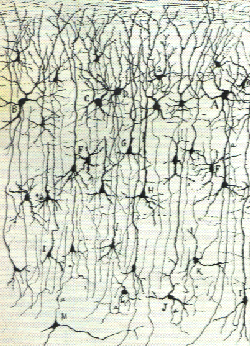
properties of interconnections networks of the brain.
| The graphic gain which the model offers is not to denigrate, for,
synchronization beams almost identical to these of our model are found
again in some other cases of networks superposition, such those obtained
by x-ray cristallography of some proteins (Laue' Figures, see appendix
D-a-1).
Opposite: Rubisco protein x-ray cristallography.
|
ex13 |
D-7-2 Correlations between chryzode and Rubisco
The possible correlations between two systems have encouraged us
to try to find whether, by the means of the chryzodes system, we could
get a figure approaching the one which is obtained in -ray-cristallography.
Opposite, one of the results. Let us note that we had to assign
the rules of an homologic inversion to each point. |
ex14 |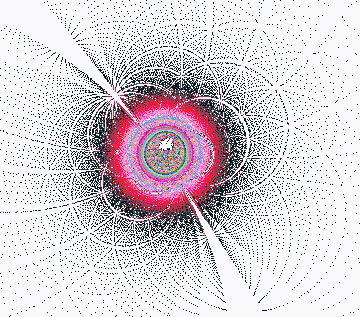
D-8- The synchronization beam envisaged as a brick of
a cognitive and behaviour management.
As a general rule, with the chryzodes system, the synchronization
beams are found in every harmonic superposition of points networks.
The emergence of these beams in chryzodes and x-ray cristallography
sets thinking. All the more so as our perception of visible has not get
us used to such a type of structure while they appear quite quickly in
the superposition of points networks (see appendix 3).Probably if
they are not directlly visible to the naked eye, it is that our visible
perception covers only one frequency scale (from red to ultraviolet,there
is only one multiplication by 2). Yet, the emergence of the beams is linked
to an harmonic growth of the frequencies (ex: 2, 8, 16, etc.).
However, we know that the auditory cortex can analyse harmonics.
The presence and the distribution of cells with a growing sensitivity in
the internal auditory meatus prove that neurons are capable of a quantitative,
qualitative and harmonic analysis. On the other hand, let's not forget
that a part of the cortex used in the sound harmonics analysis can be in
the deaf allied with some other cognitive phenomena.
Be that as it may, forced to deductive methods, it is interesting
to envisage a sort of correlation between both phenomena, that is on one
hand, the superposition of the cristallographic refractions, and on the
other one, the modelization by means of the points of intersection of the
vectors resulting from a superposition of networks.
At this stage, we have to consider that we have got a tool which gathers
solutions to the three departing problems in an only scheme.
That is to say :
-The extreme density of the neuronal system : This one is resoluted
by the fact that we are not limited in the quantity of the elements to
take into account on the circumference. The analogy with the ring of
real numbers seems to be founded.
- The fitting of the treatment and the superposition: superimposing
the various analysises on a same graph answers the difficulty. This enabled
us to extract the synchronization beams.
-Discretization of information: using vectors as a scaffolding,
and taking the only points of intersection into account, in a way just
like at the intersection of a whole of neurons, we have entered a process
partly similar to those we find in proteins x-ray cristallographies.
To extrapolate and to pursue towards the cognition mechanisms is a speculative
venture which gets us ahead forward a few steps. However, and we quickly
realize it, the task is colossal. The field of numbers is infinite, the
shapes to be listed are also infinite. As for the classical mathematical
tool, it proves to be incomplete to work out the whole of possibilities.
We should have a super Fouriers' function, and the present approach towards
the correlations by waves and the Gabors' function are in line with. As
regards chryzodes, everything is still to be done, if we leave out the
tracks left by Fermat, Pascal, Gauss and Poincare.
The bringing -in of the chryzodes makes new hypothesises likely
and to be envisaged. For example during a cognitive analysis, the system
sets up kinds of needles, axises or axises networks which take their origin
in the synchronizations resulting from the superposition of the various
levels of the information processing. This can be as by an exciting effect
of the axonal extremities as by an inhibiting effect. The beams may be
isolated and fleeting like in the case of a small sense excitation or more
intense, more concentrated, like in the case of a concentration or a philosophical
meditation.
What matter to us is that these vectors, a little like paths, memory
lines, "tubes" resulting from the synchronizations between the different
layers operating an analyis, could be instantly or subsequently (REM sleep)
used in a more vaste architectural set. We then should have a sort of "patterns"
management, in the sense defined by Jung, molds, in a way a vocabulary
and a grammar of cognition.
The difficulty is that in this type of investigation, it is quite difficult
to go directly over to testing because of aspects linked to ethics. The
more elevated in the scale of perceptions is the faculty we like to understand,
the more it is necessary to go towards analysts, philosophers, visionaries
in order to decipher their experiences in the light of our inquiring faith.
Actually, the short-term experiences are not easily possible and the searches
are long and complex. For example, before obtaining a chryzode looking
like the Rubisco, we had to analyse the process in a x-ray crystallography
to note the fitting was generating an homological inversion. On the
other hand, a biologist advised us to present the images resulting from
chryzodes to any light mentally deficients in order to study their reactions.
Some mathematicians rose an outcry when we suggested this experimentation.
It seemed to us useful then to avoid a conflictual approach.
Progressing in our research on chryzodes we have found multiple tracks.
The correlation with the synchronization beams is only the one which seems
to us the most reliable. Some other ways enable us to have a few chances
to advance. In the appendix we present the ones seeming to us the most
promising. A vast work remains to do. And though the chryzodes at this
time seem to arise more questions than these they resolve, they at least
have the advantage to offer us new senses for which had seem to be a labyrinth
of complexity.
D-9- Epistemology
Remember, chryzodes make possible to explore every function
operating on integer numbers and by approximation on real numbers.Whatever
they are, recurring decimal or complicated equation decimals,they always
show properties hidden by the abrupt austerity of an integro-differential
formalism. This is a new way to representcertain mathematical objects,
as lines and points networks, to show logical abstractions, to manipulate
a sort of alphabet of shapes.
Considering the fertility of the obtained aesthetic and rationnal results,
the system seems to be situated at an epistemologic croosroads and seems
to be able to generate a whole of possible senses. They can nourish the
everyone's imagination and creativity as in the field of research as in
the field of experimentation as well in the growing one of modelling.
We first note that from a simple arthmetico-geometrical mechanism
we get harmony, organization, but neither disorder, nor accident. The chryzodes
make possible to approach arithmetic under a new angle of view, especially
number in its simple operations, in the field of congruences or sequences.
Another important aspect seems to be the use of a circular referential
that enables to envisage a geometry of chryzodes in complement of the analyticespecially
to account for a process or a transformation. At the first glance, we understand
the power of representation of the model : the economy in the contained
information. The analogy with the ideal of the Greek mathematics in its
research of alliance between proportion and beauty here is undeniable.
We achieve the mathematical aspect of the model recognizing it as belonging
to the new branch opened by, among others, Poincare, Julia, Thom or Moulin,
and concerning chaos, disorder, catastrophes, fractals, arithmetic
relators. This conception incontestably draws near a new epistemology
with the consideration of reality as a possible "constructed" rather
than a "given" reflecting an unchanging reality. The creation of patterns
is one of the important instruments of this movement and the system of
chryzodes seems to be able to favour simulations when it 's the matter
of phenomena of a periodical or undalory nature.
With regards to the creation of shapes, one can think of an important
bringing to morphogenesis, understanding of processes and representation
of waves fields.
D-a-1- Epicycloides and hypocycloides
"A point M on a mobile circle C with radius r (generator circle) which
rolls without sliping on a fixed circle with radius (directrix) describes
out a curve L. L is called epicycloide when the contact is external and
hypocycloide when the contact is internal.
When the ratio R/r is a fraction which is in its irreducible form
p/q (q different from 1), then the epicycloide is an algebraic curve too
and it is composed of p equal branches." History
"The astronomers in ancient Greece explained the retrograde movements
of planets giving them an uniform movement following a circumference
(epicycle) the center of which moves on another circumference. The property
according to which the point of a circumference internally rolling on a
motionless circumference with a radius two times larger describes the diameter
of the motionless circumference, was independently discovered by Nassir
Eddin (middle 13th-century) and Nicolas Copernic (beginning 16th).
But the systematic study of the epicycloide and hypocycloide
started in 1525 with the Albrecht Dürer's theoretical works that remained
unknown from mathematicians.
Desargues and then La Hire, at the middle of the 17th-century, worked
out many important properties of these curves.
In its "Mathematical principles in the natural philosophy" (1687),
Newton generalized the Huyghens's researches about the cycloïdal pendulum
and he worked out that in a spherical attraction field, the isochronal
oscillations of the pendulum is the epicycloïde.
Afterwards the natural generalization of cycloïdes, epicycloïdes
and hypocycloïdes did not stop attracting the searchers'attention,
among them, Leibnitz, Euler et Bernouilli."
Texts from "Aide mémoire de mathématiques supérieures",
M Vygodsky, ed. de Moscou, 1973.
D-a-2-Method of diffraction in polychromatic radiation
There is only one method of diffraction in polychromatic
radiation and it only applies to monocrystals: this is the Laue method.
A tungsten anticathode A excited under a tension of 50 to 80 kilovolts
is used. We thus have a continuous spectrum included between between 0,2
and 2 A. An approximately parallel beam is obtained by means of two holes
a few tenths millimeters wide pierced in two lead plaques assembled at
the extremities with a metal tube. The beam falls on the crystal and the
Laue patches form on the sensible surface S. The distances from A
to D1 and from D1 to D2 approximately are of 4 or 5 cm. The crystal C is
very near from the diaphragm D2. The distance CO, from C to S varies
between 2 and 10 cm.
Each patch characterizes a family of reticular planes, except the central
patch generated by the direct beam which came across the crystal without
diffracting it.
If in the spectrum produced by the anticathode there is a wavelength
that verifies the Braggs 'hypothesis, there is a beam selectively reflected
under the angle COT (T: Laue patch).
(...)
The Laue method does not give any informations about the reticular
distances but only about the angles.
In order to show the polychromatic nature of Laue diagrams, we carried
out some colour ones with the following artifice.
Three diagrams of a same crystal are taken at different tensions:
one at 18 kilovolts without filter, the second one at 35 kilovolts with
an aluminium filter of 2 mm, the third one with an aluminium one of 4 mm.
We thus select three ranges of wavelengths that would respectively correspond
to the orangy red, green-yellow and purple-blue regions of the visible
spectrum, if they could be multiplied by 10 000. We artificially operated
this transposition using the trichromatic synthesis: each one of these
snaps is printed in a suitable colour and their superposition gives a diagram
the patches of which go from red to purple when the radiation which produced
them goes from 18 to 55 kilovolts.
Texts taken from: " Principes de radio-cristallographie" by Jean
Barraud, Masson ed., 1960, p 84 to 87
D-a-3- Details of a superposition
of networks.
Next we study two asymptomatic scenarios , that is:
1) Superposition of networks in modules multiple of a same number.
2) Superposition of networks in modules of consecutive values.
1) Superposition of networks in modules multiple of
a same number.
In the example below each layer illustrates an increasing number
of elements in interaction.
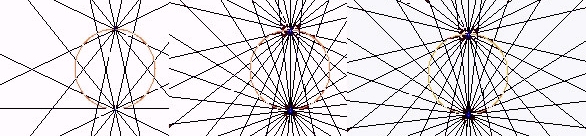
Then, let us substitute for each network in lines its network in
points of interconnection.
| Although each layer does not separately seem to have a particular
structure, on a third graph we observe that the superposition of five points
networks already makes a small set of synchronization beams emerge. |
 |
| Carrying on the process a few steps further, this one gets accentuated. |
 |
2) Superposition of networks in modules of consecutive
values
With a small interval (or not) between each number, the harmonic
beams disappear giving the place to kinematics of whirling shapes made
of a tang of waterings, curves, necks, nodes, focuses.
Multiplication by 3 in the numbers 1000, 1001, etc.
If we give a different colour to each number and we make the palette
of colours turn, we easily observe the movement of the diverse whirlwinds.
The waterings (necks, curves in layers, etc.) seem to correspond to the
partials of the wave (partials = groups of frequencies, the values of which
are consecutive ex 1001, 1002, 1003, etc.). Ex below: the details of the
superposition of the multiplication by 3 in circles with from 1000 to 1200
elements.
Of course some other powers than these of 2 or 3 can be expressed. To
vary the type of operation and the type of function leads to discover an
infinity of figures. This infinity of possible topologies and the cybernetic
levels that we easily detect would themselves require a thesis. In fact,
many other aspects are yet to be resolved. Let us sum up saying the chryzodes
graphically express arithmetical properties that can be extended to the
reals numbers by approximation. As for the structures emerging from
the different superpositions of networks , they are found in physics in
many resonance phenomena , like in the structures resulting from x-ray
cristallography or, we give an example below, in the luminous refractions
produced by a vibrating circular mirror.
D-a-4 Vibrating circular mirror
A simple example allows to approach the physical phenomena generating
figures linked to the shapes discovered by chryzodes.
Let us stand a wide circular container with a little liquid in on an
unstable rest . For example a big aluminium pan with a little water inside
and put on a rickety table. We light this container with a luminous beam
in such a way that the luminous refractions coming from the pan are reflected
on the ceiling of a dark room. At rest, we observe a simple shimmering
as it happens at the surface of an expanse of water.
Let's now animate the table with the pan by a rythmic motion.
We then observe a sort of rose with an hypocycloidic contour, on
the ceiling of the room, in the drawing of the reflections coming from
the container set on the table. |
 |
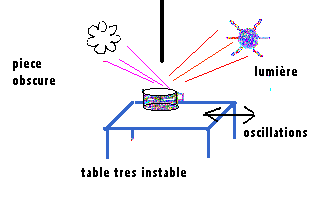Let's change the frequency of our motion, the luminous phenomenon turns
into a spiral, then it is transformed again into a new rose with a different
number of petals, once the motion is stabilized on another frequency.
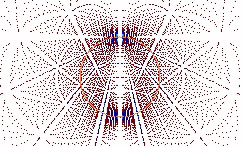
D-a-5-Superposition of couples of inverses
Vertically and horizontally going over the table of the multiples
congruent to a number, chryzodes relate kinematics of epi and hypocycloidic
topologies. Each one of these shapes is itself made of all a fractional
cycloides spectrum. These different oscillations between the intern and
the extern according to some processes of implosion-expansion can the most
of the time be summed up by the couple of inverses : a * b = 1 mod m.
At a superior level of representation, instead of drawing all the transformation
signified by a chryzode resulting from a series of powers , we can identify
the process by a simple line connecting the verse term to its inverse,
on a new chryzode.
In the example 6 previously seen and that relates the power of 2
transformations into powers of 10 when they are congruent to number 19,
we only have to connect the point 2 to the point 10 on a circumference
divided into 19 points.
It is then useful to represent the other verse-inverse couples of
number 19, what is easily obtained by calculating the powers N-2 of the
number.
For 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18, etc., we have:
1 10 13 5 4 16 11 12 17 2 7 8 3 15 14 8
that are the verse-inverse couples:
2*10, 3*13, (4*5), (5*4), (6*16), etc.
In a new chryzode, these different couples are represented by the
means of vectors connecting the terms of each couple.
A more exhaustive study makes the chryzode appear modelizing the
couples of inverses as a sort of "identity card" summing up a certain number
of arithmetical properties of number 19. |
 |
Contrary to the chryzodes resulting from the multiplications in which
the presence of hypocycloidic curves seem to be an invariant, the structures
of the chryzodes representing the couples of inverses seem to be geometrically
different from each other.
Below, we have represented the couples of the inverses of numbers
232 to 235.
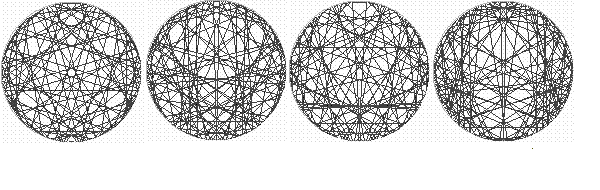
| Yet, and surprisingly, constructing the superposition of the couples
of inverses of a quite large sequence of consecutive modules, we notice
the multitude of distinct shapes is joined, jointed in an unique structure.
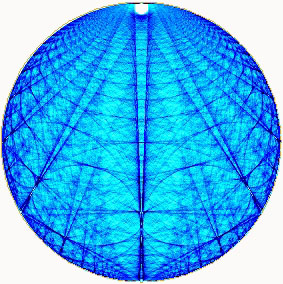
Opposite, see the superposition of the identity chryzodes from 5
to 50 in a same circle. |
 |
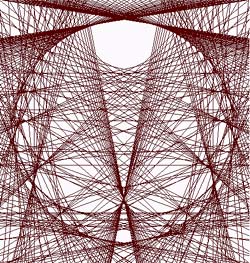| Finally let us say that this type of new shape looks a little like
a shell in the first stages of its construction, but very quickely this
shape fades for a topology not yet classified.
Example opposite: we have superimposed every vector representing
the couples of inverses of the numbers from 5 to 236. |
 |
In an attempt of an exhaustive approach of the field, this topology
would seem to be like a fundamental lighthouse, a sort of informative field
skeleton, a sort of central pivot. The poet would maybe see here a key
giving the access to many other topologies, that could be to some extent
called computing, so much close are the interrelations to the image
of the interrelations between the different levels of the mathematical
abstraction.
D-a-6 Comparison between the Helmotz curve and chryzode
Finally let's cite an interesting parallel between the position and
the intensity of the internal peaks of inflection of the star polygons
superposition in a chryzode (split into two) and the Helmotz consonance
curve. The latter is worked out from the harmonious concordance between
a C sound and another sound generated by a musical string going from this
C up to the C of the superior octave.
| We note the resonance troughs of the Helmotz 's graph correspond
to the half-chryzode peaks of inflection. Thus, we discover a surprising
correlation of structure between the peaks of inflection of the hypocycloidic
curves of the chryzode representing the integers series and the resonance
chords of the musical scale (represented by the troughs of the helmotz's
curve) in relation to the initial C. |
 |
Concluding the appendix D
The chryzodes described in this presentation only are the first letters
of an alphabet of shapes and many other structural processings are applicable
for each aspect of a structural resonance. In life experience, the organization
of things is much more subtle than all the possible rationalizations (fortunately!).
Life modifies models, moulds, at its convenience, however respecting some
constraints. Yet, for as simple as the chryzodes are, they are not to be
neglected: they have many analogies of organization in relation to our
logic of perception and in the present neurophysiological research diverse
indications are found tending to support the incidence of such an organization
within our brain. The similitude of the vectorial decodings must not escape
us, all the more so as chryzodes are themselves a logical way of decoding.
Apparently, the visual cortex of monkeys shows a marked preference of analysis
for the angles 10 degrees apart. In a chryzoidic application, we could
say the monkey's prefered relator is a chryzoidal ring with 32 different
angles, that is an exponential base (power of..) 37. This is only a rudimentary
way of envisaging some more succinct fields of application.
BIBLIOGRAPHY OF THE APPENDIX D
"Le Cerveau" ; Ed. Pour la Science, nov. 1979.
"La Recherche", Laure Schachli, december 1991.
" Principes de radio-cristallographie", Jean Barraud,
Masson ed., 1960, p 84 to 87.
"Les Nombres Premiers " ; J. Itard : PUF.
"Hypocycloïdes et Epicycloïdes" ;J. Lemaire
: Libr. Blanchard.
"Théorie des Nombres" ; E. Lucas : Librairie
Albert Blanchard.
"Aide Mémoirede Mathématiques Sup."
; M. Vygodski : Ed. Mir.
"Aide Mémoire de Physique" ; B. Yavorski et
A. Detlaf :Ed. Mir.
"Actes Congrès MATh.
en. JEANS. 1996", Pierre Duchet ; ed MATh en JEANS, Paris
"Eurêka",Helène Prost, décembre 1995, Bayard
Presse, Paris
"Encyclopedia of World Problems & Human Potential ", Anthony Judge, 1994, ed
U.I.A., Bruxelles
"Journées nationales APMEP 1993", Pierre Germain, Jean-Paul
Sonntag, ed. APMEP, Paris
"Science en Fête 1993", Corinne Rouiller, Pierre Germain,
Jean-Paul Sonntag, Ministère de la Recherche, Paris
"Second European Congress on Systems Science in Prague- Proceedings",
1993, ed. UES.-AFCET, Pierre Germain, Corinne Rouiller.
"U.A.T.I., n 1", Marcel Locquin, 1993, ed. UNESCO,
Actes Congrès "MATh.
en. JEANS. 1993", Pierre Audin, ed MATh.en.JEANS, Paris
"Actes
Congrès International UITF 1992", Corinne Rouiller, Jean-Paul
Sonntag, ed UITF, Paris
"Actes
Colloque Systema 1992", Pierre Germain, Jean-Paul Sonntag, AFCET, Paris
